Demonstration of Superposition Theorem & Examples

Superposition Theorem Principle

In a network of resistors the current in any resistor Is equal to the algebraic sum of the currents delivered by each independent sources assuming that each source is acting alone or independently with respect to the others

Note :
If a source either a current or a voltage source) is acting alone the other current sources are open circuited while the other voltaae sources are short Circuited.

Superposition Theorem steps  Demonstration :

Step 1: 

If E1 is acting alone.

step 2: 

If E2 is acting alone.

Note : 

The current I1' , I2' , I3' , I1" , I2" & I3" are evaluated using basic electric circuit principle


I1 = | I1' + I1'' |      I2 = | I2' + I2'' |      I1 = | I3' + I3'' |

Solved problem :

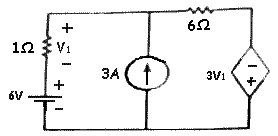
Determine the current in the 6 ohm resistor using Superposition Theorem

1. 3.4 A
2. 4.2 A
3. 4.0 A
4. 3.8 A

Solution :

Note about this Exemple :

whene a source is operating alone, the other current sources must be opened while the other voltage sources must be short circuited

let the voltage source to operate alone.

Apply KVL :

6+V1-I'(6) + 3V1=0
6+4V1 = 6I'1   Equation 1
V1I'=(I1= I'    Equation 2

substitute E.q.2 in E.q.1:

6 +4(I') = 6I'
I' = 6/2 = 3A
I' = 3A

Let the current source to operate alone.

Apply KCL at node 'a':

3 = I1 + I"
3 = V1/1+((V1 + 3V)/6)
3 = 1.667.V1

V1 = 1.8V

I"=(4V1/6) = ((4x1.8)/6 = 1.2 A

I = I' + I" =3 + 1.2

I = = 4.2 A

Note : Since the direction of currents of both I' and I" are the same, then the resultant current that will flow in the 6 ohm resistance, is equale to the arithmetic sum of the two currents respectively.